Breaking Down: Tic-Tac-Toe

Joshua Cole - 11 Aug 2016

(Editor’s Note: Keep in mind as you’re reading, this post is an executable Eve program. See the raw text here. This is our first example of literate programming in Eve, so let us know what you think!)

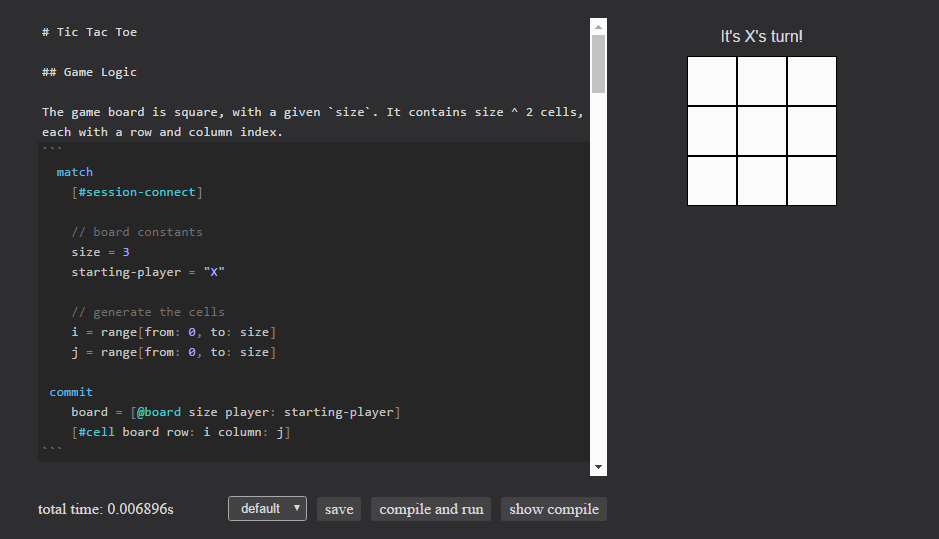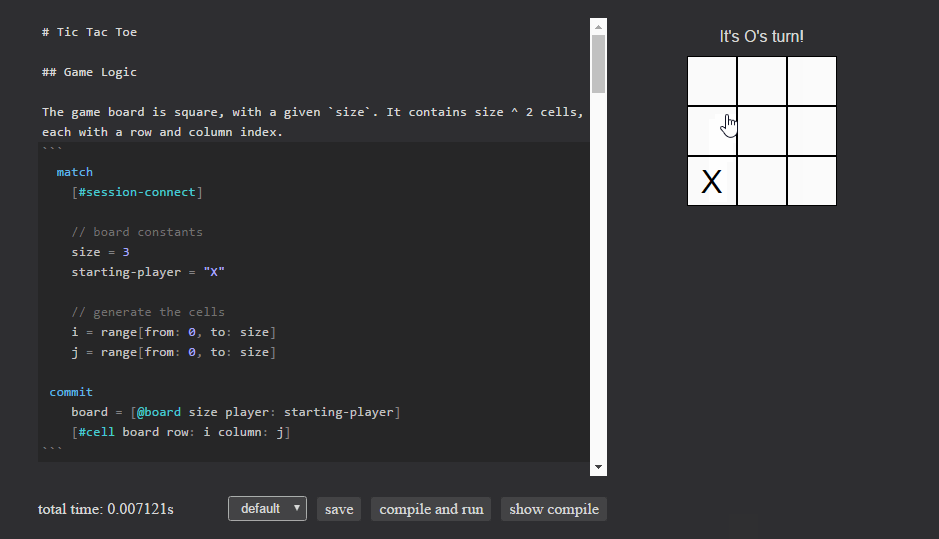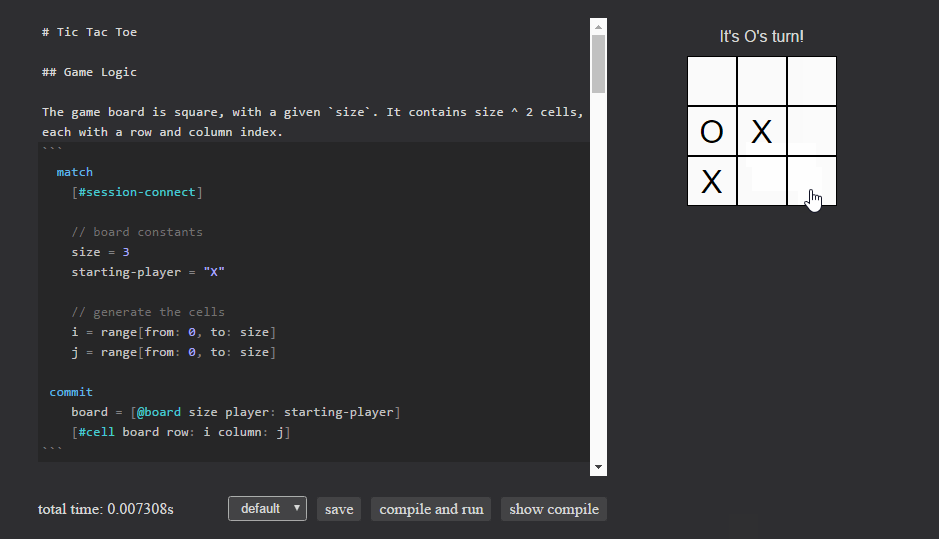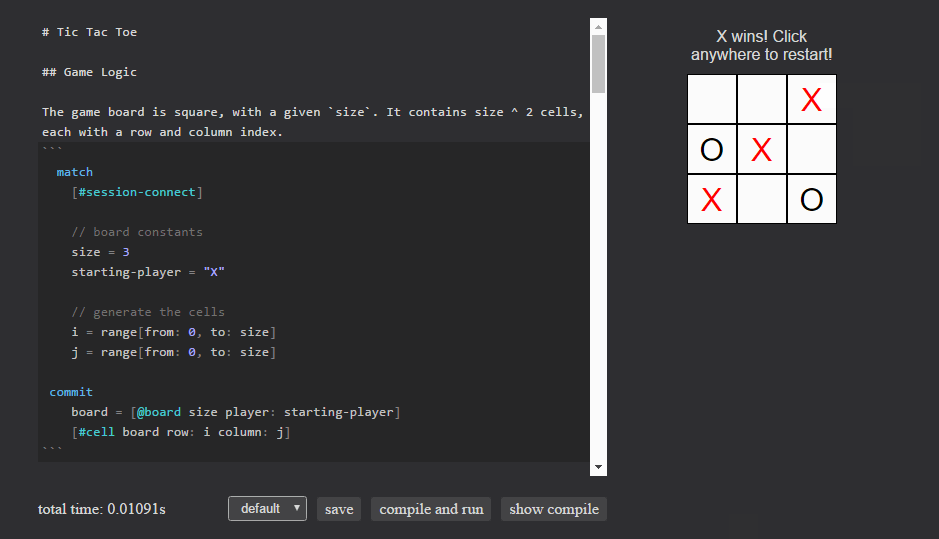
Last week on the mailing list, RubenSandwich posted an interactive demo capable of playing and scoring tic-tac-toe searches. He provided some great feedback about the issues he ran into along the way. Now that the language is becoming more stable, our first priority is seeing it used and addressing the problems that surface. To that end, his troubles became our guide to making Eve a little friendlier for writing interactive applications in general. Today we’ll look at a simplified version of tic-tac-toe that takes into account his feedback.

This analysis (and future breakdowns) will be written inline in Eve to make the discussion flow more naturally. Since Eve is a superset of GitHub-Flavored Markdown which our blog is capable of rendering, we can provide a pleasant reading experience directly from the source code.

Game logic

Tic-Tac-Toe is a classic game played by two players, “X” and “O”, who take turns marking their letter on a 3x3 grid. The first player to mark 3 adjacent cells in a line wins. The game can potentially result in a draw, where all grid cells are marked, but neither player has 3 adjacent cells. To build this game in Eve, we need several parts:

• A game board with cells
• A way to mark a cell as “X” or “O”
• A way to recognize that a player has won the game.

To begin, we initialize the board. We commit an object named @board to hold our global state and create a set of #cells. These #cells will keep track of the moves players have made. Common connect-N games (a generalized tic-tac-toe for any NxN grid) are scored along 4 axes (horizontal, vertical, the diagonal, and the anti-diagonal). We group cells together along each axis up front to make scoring easier later. This process is made much cleaner by the addition of new math expressions like range[from, to]. This is a small part of our effort to expand the standard library based on usage. If you’re interested in helping shape this, stop by our RFCs repository or jump right in on our discussion of standard string expressions.

The game board is square, with a given size. It contains size ^ 2 cells, each with a row and column index.

search
  [#session-connect]

  // board constants
  size = 3
  starting-player = "X"

  // generate the cells
  i = range[from: 0, to: size]
  j = range[from: 0, to: size]

commit
  board = [@board size player: starting-player]
  [#cell board row: i column: j]

A subtlety here is the last line, [#cell board row: i column: j]. Thanks to our relational semantics, this line actually generates all 9 cells. Since the sets of values computed in i and j have no relation to each other, when we use them together we get the cartesian product of their values. This means that if i = {0, 1, 2} and j = {0, 1, 2}, then i x j = {(0, 0), (0, 1), ... (2, 1), (2, 2)}. These are exactly the indices we need for our grid!

Now we tag some special cell groupings: diagonal and anti-diagonal cells. The diagonal cells are (0, 0), (1, 1), and (2, 2). Notice anything about them?

Diagonal cells have a row index equal to its column index

search
  cells = [#cell row column]
  row = column
bind
  cells += #diagonal

Similarly, the anti-diagonal cells are (0, 2), (1, 1), and (2, 0).

Anti-diagonal cells satisfy the equation row + col = N - 1, where N is the size of the board.

search
  cells = [#cell row column]
  [@board size: N]
  row + column = N - 1
bind
  cells += #anti-diagonal

A game is won when a player marks N cells in a row, column, or diagonal. The game can end in a tie, where no player has N in a row.

search
  board = [@board size: N, not(winner)]
                    // Check for a winning row
  (winner, cell) = if cell = [#cell row player]
                      N = count[given: cell, per: (row, player)] then (player, cell)
                    // Check for a winning column
                    else if cell = [#cell column player]
                      N = count[given: cell, per: (column, player)] then (player, cell)
                    // Check for a diagonal win
                    else if cell = [#diagonal row column player]
                      N = count[given: cell, per: player] then (player, cell)
                    // Check for an anti-diagonal win
                    else if cell = [#anti-diagonal row column player]
                      N = count[given: cell, per: player] then (player, cell)
                    // If all cells are filled but there are no winners
                    else if cell = [#cell player]
                      N * N = count[given: cell] then ("nobody", cell)
commit
  board.winner := winner
  cell += #winner

We use the count aggregate in the above block. Count returns the number of discrete values (the cardinality) of the variables in given. The optional per attribute allows you to specify groupings, which yield one result for each set of values in the group.

For example, in count[given: cell, per: player] we group by player, which returns two values: the count of cells marked by player X and those marked by O. This can be read “count the cells per player”. In the scoring block, we group by column and player. This will return the count of cells marked by a player in a particular column. Like wise with the row case. By equating this with N, we ensure the winning player is only returned when she has marked N cells in the given direction.

This is how Eve works without looping. Rather than writing a nested for loop and iterating over the cells, we can use Eve’s semantics to our advantage.

We first search every row, then every column. Finally we check the diagonal and anti-diagonal. To do this, we leverage the #diagonal and #anti-diagonal tags we created earlier; instead of selecting [#cell], we can select on [#diagonal] and [#anti-diagonal] to select only a subset of cells.

React to Events

Next, we handle user input. Any time a cell is directly clicked, we:

1. Ensure the cell hasn’t already been played
2. Check for a winner
3. Switch to the next player

Then update the cell to reflect its new owner, and switch board’s player to the next player.

Click on a cell to make your move

search
  [#click #direct-target element: [#div cell]]
  not(cell.player)                               // Ensures the cell hasn't been played
  board = [@board player: current, not(winner)]  // Ensures the game has not been won
  next_player = if current = "X" then "O"        // Switches to the next player
                else "X"
commit
  board.player := next_player
  cell.player := current

Since games of tic-tac-toe are often very short and extremely competitive, it’s imperative that it be quick and easy to begin a new search. When the game is over (the board has a winner attribute), a click anywhere on the drawing area will reset the game for another round of play.

A reset consists of:

• Clearing the board of a winner
• Clearing all of the cells
• Removing the #winner tag from the winning cell set

search
  [#click #direct-target]
  board = [@board winner]
  cell = [#cell player]
commit
  board.winner -= winner
  cell.player -= player
  cell -= #winner

Drawing the Game Board

We’ve implemented the game logic, but now we need to actually draw the board so players have something to see and interact with. Our general strategy will be that the game board is a #div with one child #div for each cell. Each cell will be drawn with an “X”, “O”, or empty string as text. We also add a #status div, which we’ll write game state into later. Our cells have the CSS inlined, but you could just as easily link to an external file.

Draw the board

  search
    board = [@board]
    cell = [#cell board row column]
    contents = if cell.player then cell.player
              else ""
  bind
    [#div board @container style: [font-family: "sans-serif"], children:
      [#div #status board class: "status", style: [text-align: "center", width: 150, padding-bottom: 10]]
      [#div class: "board" style: [color: "black"] children:
        [#div class: "row" sort: row children:
          [#div #cell class: "cell" cell text: contents sort: column style:
            [display: "inline-block" width: "50px" height: "50px" border: "1px solid black" background: "white" font-size: "2em" line-height: "50px" text-align: "center"]]]]

Winning cells are drawn in a different color

  search
    winning-cells = [#cell #winner]
    cell-elements = [#div cell: winning-cells, style]
  bind
    style.color := "red"

Finally, we fill the previously mentioned #status div with our current game state. If no winner has been declared, we remind the competitors of whose turn it is, and once a winner is found we announce her newly-acquired bragging rights.

Display the current player if the game isn’t won

  search
    status = [#status board]
    not(board.winner)
  bind
    status.text += "It's {{board.player}}'s turn!"

When the game is won, display the winner

  search
    status = [#status board]
    winner = board.winner
  bind
    status.text += "{{winner}} wins! Click anywhere to restart!"

Along the way to making this demo, many new standard library expressions were added, the execution strategy for aggregates was overhauled, parser bugs were fixed, and dependency ordering glitches resolved. We even began to appreciate how literate programming will work in Eve (the post you are reading right now is an executable Eve program).

The human-compiled version of tic-tac-toe was completed in only about half an hour, and required very few changes to get working once the platform caught up. The latest iteration of Eve is still very much in its infancy, but even now its showing a lot of promise for teasing out simple and general solutions to complicated problems. As one of its creators, I’m obviously a biased party when discussing Eve, so feedback such as RubenSandwich’s is invaluable in helping us make the language more robust. If you find the time to try Eve yourself, please don’t hesitate to share your experiences with us on the mailing list.